高校入試で役立つ公式・定理 平面図形編 ・この公式集について この公式集は高校入試で数学を必要としている全ての受験生が利用できるように作りま した。それゆえ教科書に載っているような基礎的な内容から、中学範囲を超えた知識を利数学a 図形の性質「平面図形」 ~高校数学のまとめ~ 教科書をもとに定義や定理を独自にパネル形式でまとめています. 何度も書き直し,加筆修正を繰り返しており,完成したものではありません. このノートについて hoka95 平面図形 円 円に内接する四角形 円周角 方べき 接弦 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすること

中1 数学 中1 80 空間内の平面と直線 Youtube
数学a 平面図形
数学a 平面図形-数学a /図形の性質「空間図形」 6 / 11 平面の表記 a b c 一直線上にない3 点a,b,c があるとき, その3 点を通る平面がただ1 つに決まる. この平面を 平面abc という. 平面の決定条件 空間において 次のうち1 つが与えられると,それらを満たす平面がただ1 つに定まる. 1 2 3 4平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める おうぎ形2_半径と弧から,面積を




中1数学 平面図形 を攻略する3つコツ Qikeru 学びを楽しくわかりやすく
数学Aの教科書に載っている公式の解説一覧 まとめ 更新日時 数Aの教科書(新課程)に載っている公式(や定義など)を整理しました。 新課程では三分野から二分野選んで学習するシステム になっていますが,(多くの大学で)入試を突破するに高校数学A 平面図形 平面図形は受験における位置づけが難しい分野である。 重要か否かと聞かれたら重要であると答えざるを得ない。 大学入試共通テストでは平面図形が1つの大問として出題される ことが決まっているからである。 ただし、選択問題である。 一方、2次記述試験では平面図形の重要さは大きく減少する。 強制的に出題者の想定する解法に誘導される大学入試共通テストとは異なりも、ここで 「平面図形 」の入試問題 を分析 し、これからの 受験指導 に生かすことは 大切 であると 考 えている 。 4.研究内容 ・方法 現行課程対応 の2年分 の入試問題 のうち 、その 出題内容 の主たる 部分 が、数学 A「 平面図形 」の
折れ線の最短距離は、線対称な位置に点をずらし、直線で結ぶことで求まります。 この記事では、なぜその作図方法が最短になるのかを証明します。 Ⅰ 最短距離の作図方法 Ⅱ 最短になる理由 Ⅰ 最短距離の作図方法 今回扱う問題は、次のような問題です。方 べきの 定理とは, 平行でない 2 本の直線と円とが交わって(接して)できる図形の辺の長さの関係 を示している公式です。基本的には 3 つの形があります。 どれも三角形の相似から証明することができます。 ① 2 つの直線の交点が円の内部にあるとき このとき, が成り立ちます。数学a「平面図形」<三角形の性質> (2)学習内容 ア 三角形の角の二等分線と比 (3)教材の目的 ① 身近な事象の導入により,数学に対する興味・関心を高めること ② 「三角形の角の二等分線と比の性質」の有用性の感得 (4)指導時期案
単元 平面図形, キーワード 数学,内分,外分,重心,外心,内心,メネラウスの定理,方べきの定理,先輩ノート,証明,平行四辺形の性質,数a p67 問1,角の二等分線,math 勉強ノート公開サービス。30万冊を超える大学生、高校生、中学生のノートをみることができます。学年別指導案の例(高校1年生) 1.単元名:数学A 平面図形,数学Ⅰ 図形と計量 2.対 象高校1年生 3.教材について 三角形の頂角の二等分線の長さを,これまでの学習内容を活用し多様な方法で求める。数学Aの平面図形、空間図形の分野はほとんどが中学生の範囲の復習です。 分からない方は、中学生の範囲からやり直しましょう。 – 41 三角形の五心 – 42 三角形の定理や性質 – 43 円に関する定理




中1数学 平面図形 中学生 数学のノート Clearnote
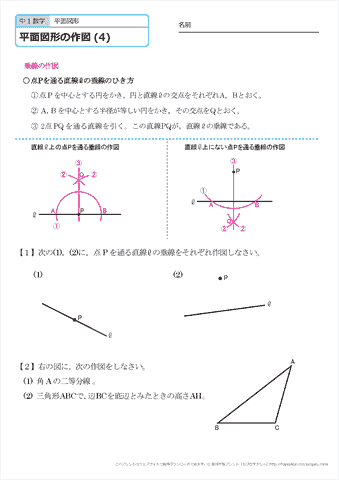



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
数学 図はab=6,ae=3で、gbを直径とする円と直線efの交点をpqとし、oから直線efにひいた垂線の足をhとしています。三角形agbとpgbはgbを軸として対称です。 このとき、hf=3数学A 第2章 図形の性質 第1節 平面図形 1限目 P62~P64 三角形の辺の比 2限目 P65~P69 三角形の外心・内心・重心 3限目 P70~P71 チェバの定理 4限目 P72~P74 メネラウスの定理 5限目 P75~P78 円に内接する四角形 中学生必見! 数学の無料プリント~復習にどうぞ(平面図形)~ 学校もまだ休校というところもあり、学校の宿題もたくさん出されたことでしょう。 ただもう終わったとか、もしかすると宿題すら出ていないという人もいるかもしれません。 そこで




世界一わかりやすい数学問題集中1 5章 平面図形




数学平面図形のコツ 入試必出の平面図形問題の解き方がわかる 秀英books 今春幸久 本 通販 Amazon
ホーム >> 平面図形 九点円の定理 角の二等分線の性質と二等分線の長さ パップスの六角形定理 三角形の合同条件 方べきの定理の証明と例題 チェバの定理とその逆 トレミーの定理とは 多角形の内角 数学 数学A・平面図形 「 ABCにおいて、AB=6、BC=7、CA=7である。この三角形に内接する円があり、辺ABと内接円との接点をMとするとき、線分AMの長さを求めよ。」です。 よろしくお 質問No平面図形がわからない人へ 中1数学「平面図形」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「図形の呼び方と移動」に関する5のポイントを覚える 「基本の作図」に関する6のポイントを覚える まずはこれらのポイント




年センター試験 数学 A 第5問 平面図形 大学入試数学の考え方と解法




センター 17年 数学ia 追試 第5問 平面図形 東大数学9割のkatsuyaが販売する高校数学の問題集
空間図形において,全ての面が合同な正多角形からなり,各頂点に集まる辺の数が全て等しい多面体のことを 正多面体 regular polyhedronという. ↑ たとえば,正四面体は正多面体であるが,正四面体2つを重ねてできる六面体は,頂点に集まる辺の数が3つの5章 平面図形 愛知県公立高校入試(数学) ~単元別過去問~ 問題プリントと解答・解説 ホーム 情報&分析 オンライン・ICT 公立対策 私立対策 国立高専 定時制 単元別 図形の美しい3つの定理〜逆数の和〜 逆数の和に関する平面図形の美しい定理を3つ紹介します。実用的な定理ではありませんが,証明はよい練習問題になるのでトライしてみてください! → 図形の美しい3つの定理〜逆数の和〜
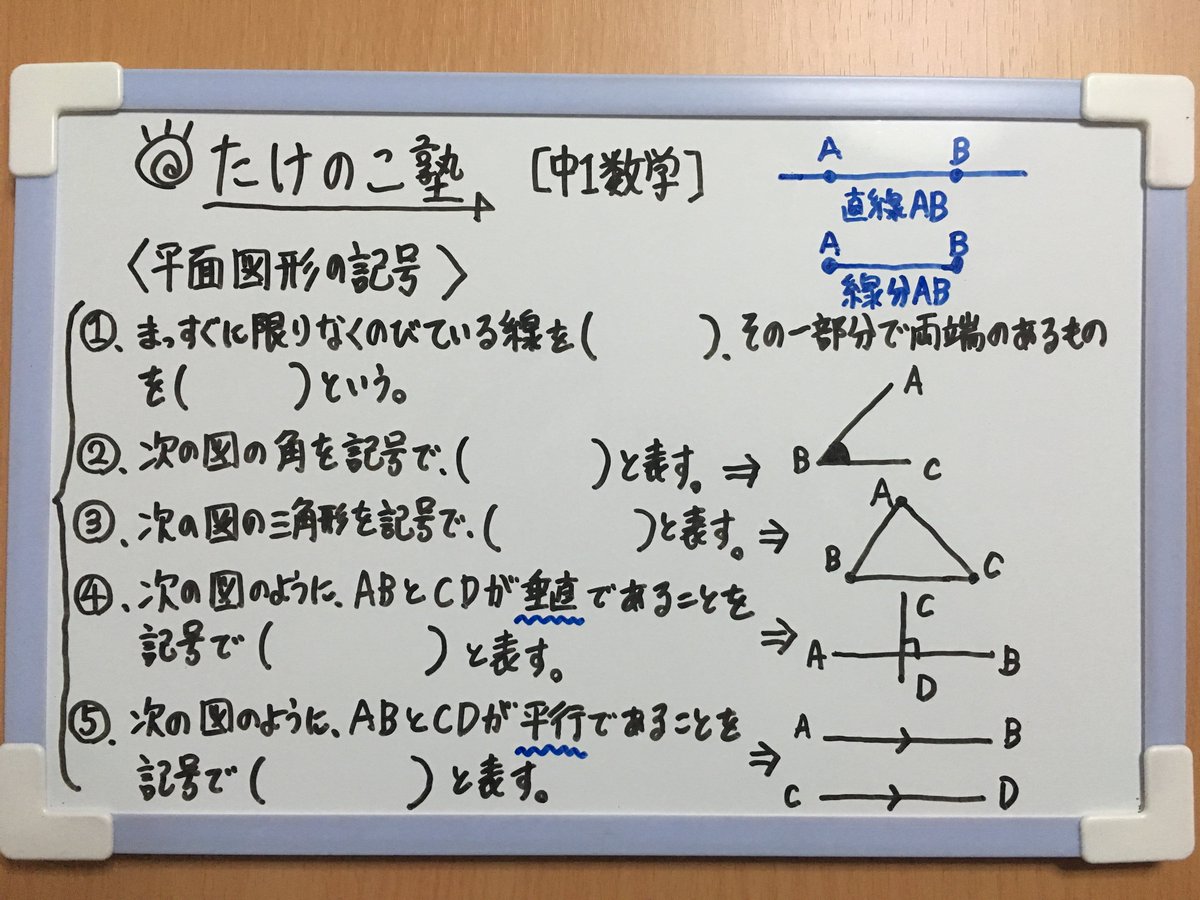



Twitter पर たけのこ塾 中1数学 今回は 平面図形の記号 についての問題です 今回の内容は以下の通りです 直線と線分 角を表す記号 三角形を表す記号 垂直を表す記号 平行を表す記号 勉強垢 中1 数学 平面図形




高校数学a 三角形の五心 三角形の内心とその存在証明 受験の月
平面・空間図形 1817 中1数学投影図ってなに??練習問題にも挑戦! 平面・空間図形 3分でなるほど!次に、この点A'と点Bを線で結びます。 このとき、A'Bと直線 が交わるところに点を取ります。 すると、この点が 最短距離になる点なのだ! ! ということで作図完成です。 最短距離の作図手順 直線に対して垂線を引き、対称となる場所に点を取る平面図形 ア 基本的な作図とその活用 「図形」は、「数と式」「関数」「資料の活用」と比較して、 最も理解しやすい分野といえますね! なぜなら、自然の摂理と同じだからです、イメージがしやすいのです! 「- (マイナス)」なんて人間の考えた基準は出てきません! 点数の稼ぎどころと言えますね! 図形のポイントは、1、2、3年生を通じて、 です! 図形の各部名称 まずは、憶えるとこは憶え




世界一わかりやすい数学問題集中1 5章 平面図形




面白い算数問題 中学受験 中学入試 算数 解説 平面図形 面積 Youtube
数学Aの平面図形で使う定理の一覧 三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 角の二等分線と辺の比の証明 三角形の外角の二等分線と辺の比 AB≠ACである ABCにおいて、∠Aの外角の二等分線と辺BCを延長した線との交点をPとする。 このとき点Pは、辺BCをAB:ACに外分する。 三角形の外心 三角形の3つの辺そ円と直線が同一平面状に存在するときには, ・ 2 点で交わる ・ 接する ・ 離れている の 3 つの場合が考えられます。 ここでは接するときを考えていきます。 円に接する直線のことを円の接線といいます。 また,このときただ 1 つの共有点のことを接点 といいます。 数A:平面図形のpdfを改訂(三角形関連に証明の追加など)。 21/7/9 数A:整数の全面改訂を完了し、pdfの販売を開始。 21/7/9 数学の全pdfを簡易的な目次を追加した最
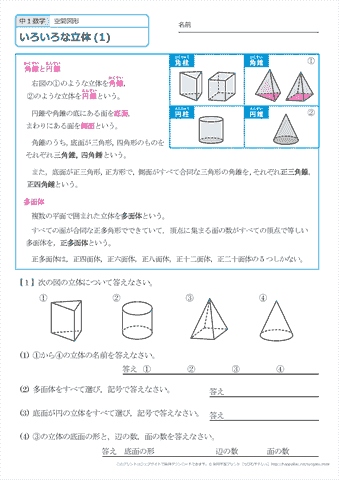



中学1年生 数学 空間図形 いろいろな立体 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学図形 高校入試レベルの平面図形の面白い問題 Youtube




中学数学平面図形 公立高校入試の良難問 定期テストや高校入試に レオンの中学数学探検所



中学数学平面図形 Apppicker




ひらめきに頼らず中学数学の図形問題を解く7つのコツ




数学 平行 と 線分比 の関係についてまとめました 知っておくと応用がきくよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



中学数学平面図形 By Takatoshi Fukino
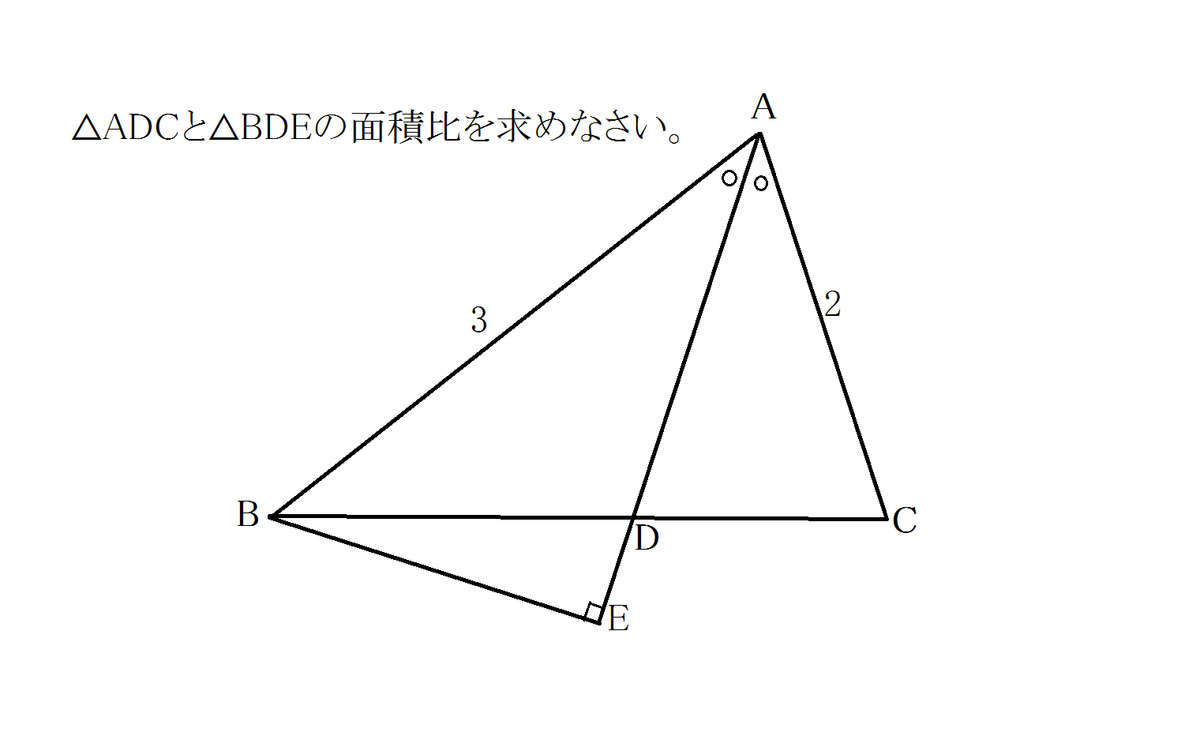



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所
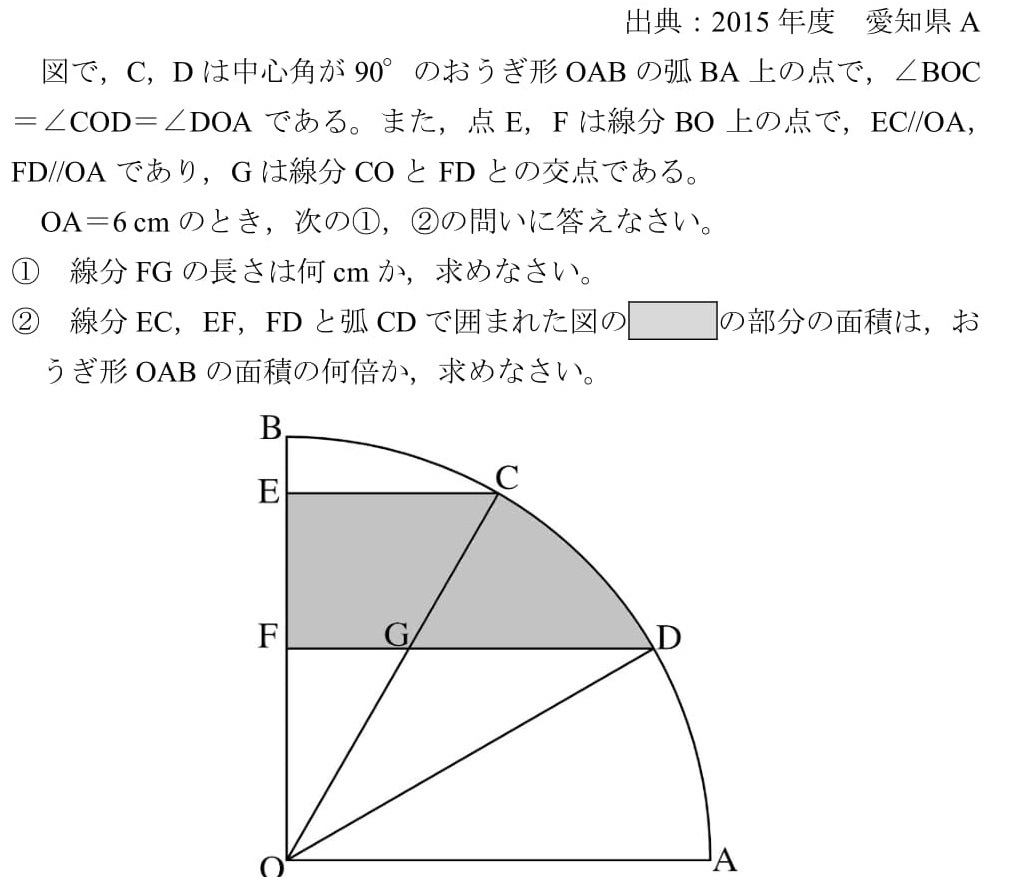



高校入試パズル平面図形 15愛知県 高校入試 数学 良問 難問
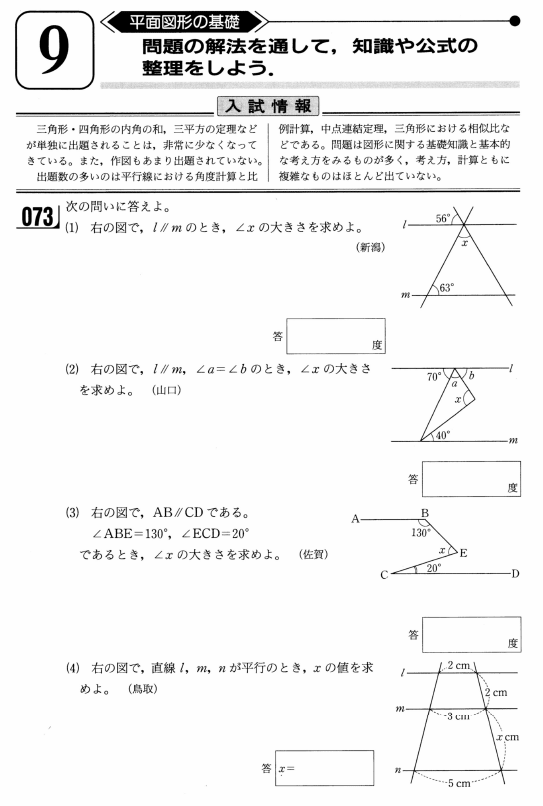



平面図形の基礎 英語 数学 さくら教育研究所 中学 高校受験 Skredu




中学 数学 実力テスト 過去問 平面図形と証明 問題と解答 赤城 ᐡᐤᐡ
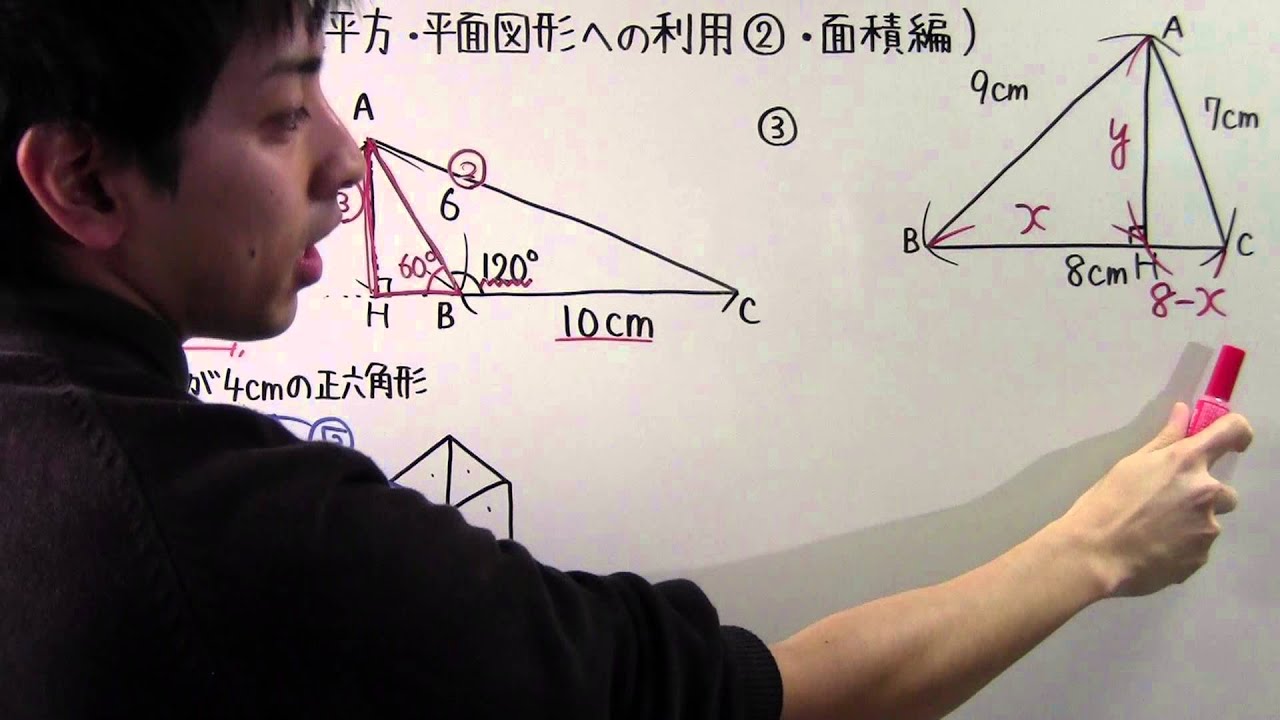



数学 中3 64 三平方 平面図形への利用 面積編 Youtube




数学 図形問題を得意にする方法 下高井戸校ブログ 中学 高校 大学受験個別指導塾testea テスティー
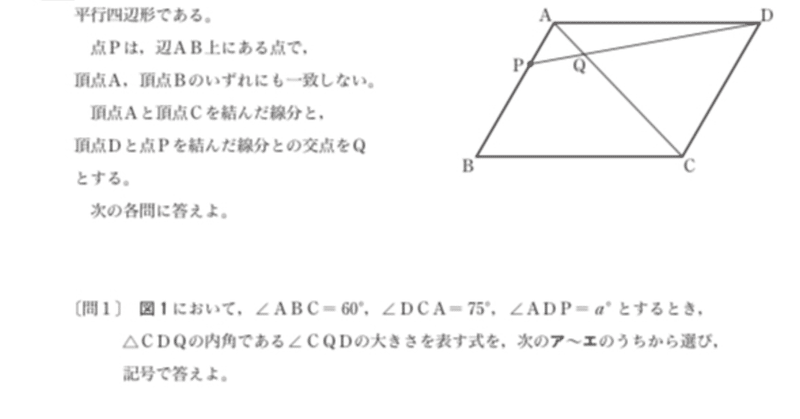



都立高校入試数学大問4平面図形 角度 対策 坂本良太 Note
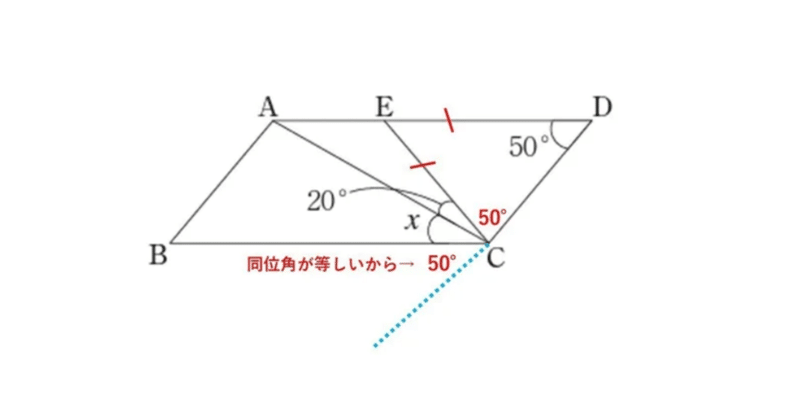



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学 Note




平面図形 高校入試 数学 良問 難問




中1 平面図形 直線に関する専門用語 右脳で覚えよう 教えたい 人のための 数学講座



中1数学テスト対策問題26 平面図形2 作図 おうぎ形 プリント
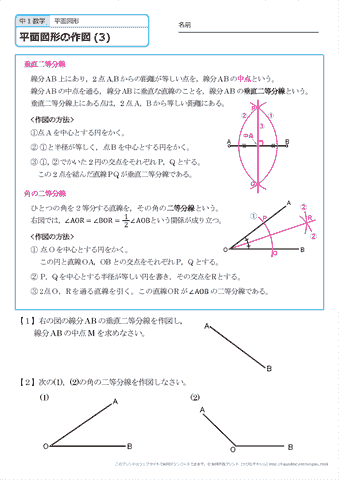



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




図形の性質 平面図形 まとめ 練習問題解説付き 高校生 数学のノート Clearnote




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント




Lt Div Gt 中学 数学 平面 図形 6623 中学 数学 平面 図形 難問



1



1



Paypayフリマ プロが教える 数学 中学 1年 Dvd 5 平面図形 基礎編 問題集
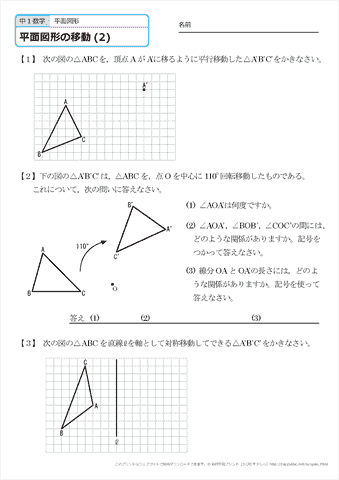



中学1年生 数学 平面図形の移動 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中3 63 三平方 平面図形への利用 基本編 Youtube
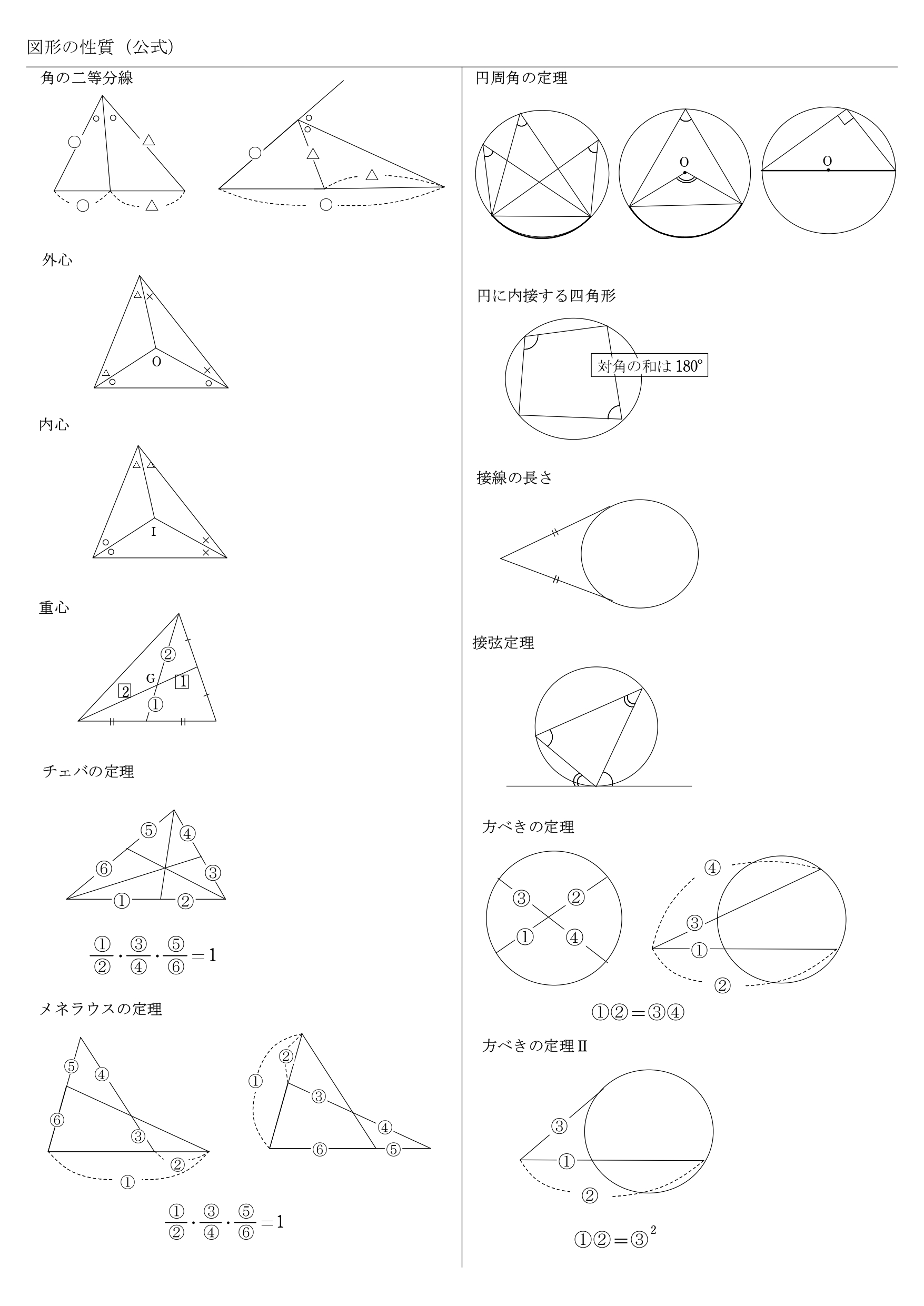



高校数学a 図形の性質 公式一覧 チェバ メネラウス 接弦 方べき 学校よりわかりやすいサイト
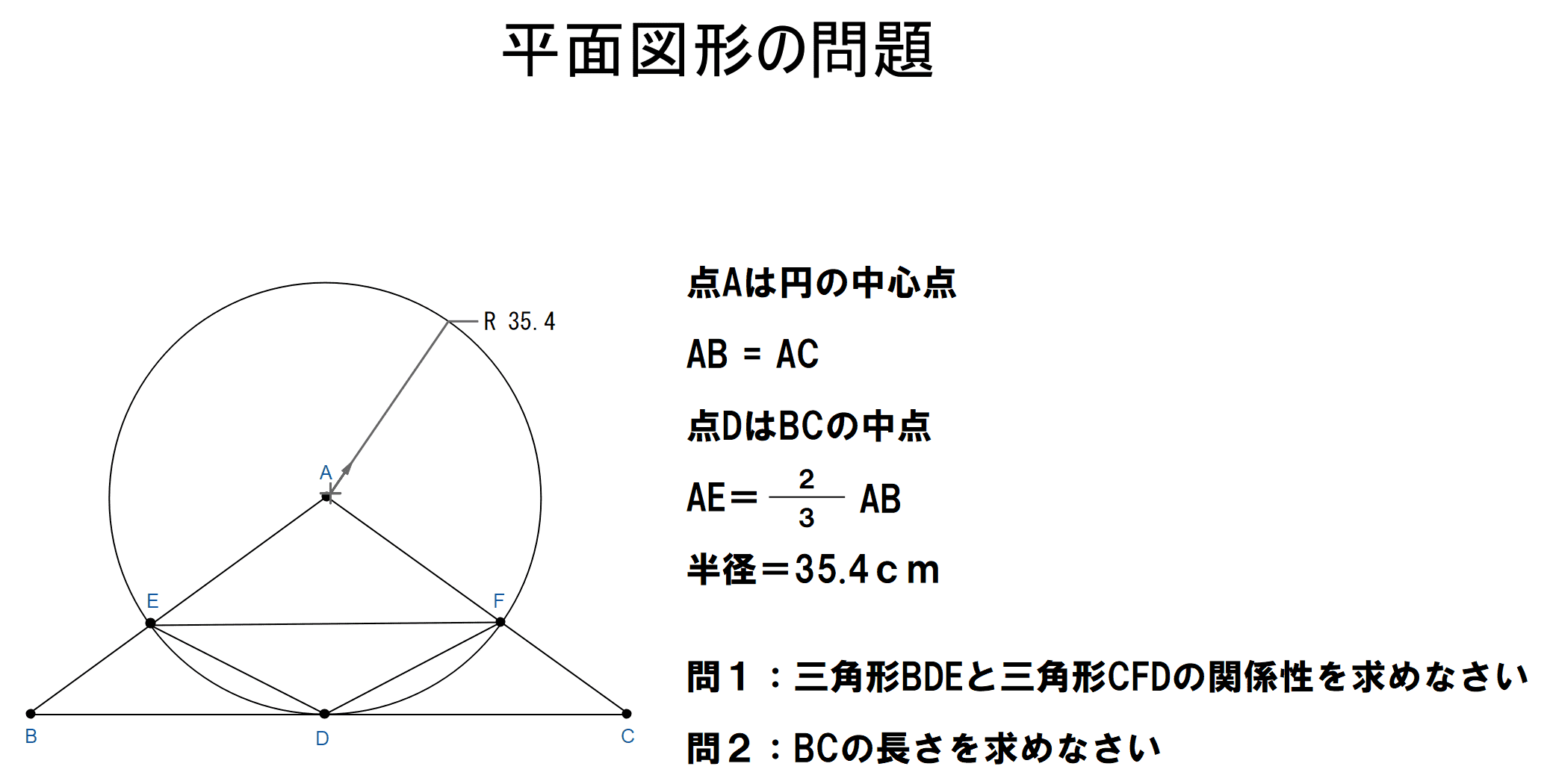



数学教師向け 平面図形問題の作成ための無料作図ソフト



中1数学 発展 応用問題プリント 平面図形のおうぎ形の弧と面積 138
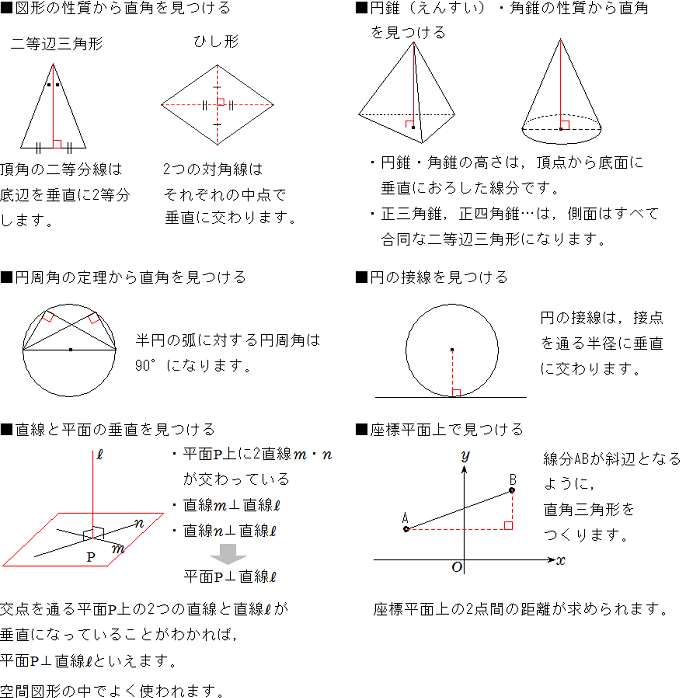



三平方の定理 平面図形 空間図形で三平方の定理を使って解くときの補助線のひき方 中学数学 定期テスト対策サイト




中1数学 平面図形 を攻略する3つコツ Qikeru 学びを楽しくわかりやすく




中1 数学 平面図形 中学生 数学のノート Clearnote



平面図形の難問1 日大豊山中




これで点が取れる 単元末テスト中1数学 6章 空間図形




高校受験 数学テーマ別攻略 平面図形 と立体図形の続き 日比谷高校のススメ



中学数学平面図形 Apppicker



中学数学の平面図形の最高レベルに難しい問題が載っているサイトや問題 Yahoo 知恵袋




平面図形 Twitter Search Twitter



無料 中1数学 基本解説 問題プリント 平面図形4 平面図形の作図 136




これで分かる 平面図形 中学生 数学のノート Clearnote
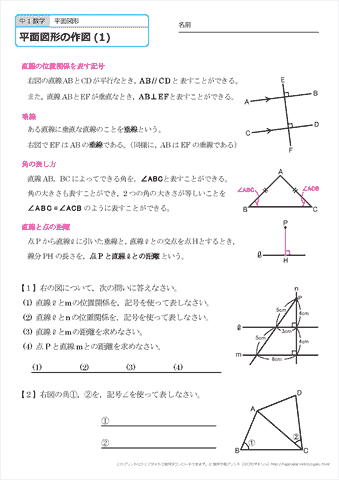



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
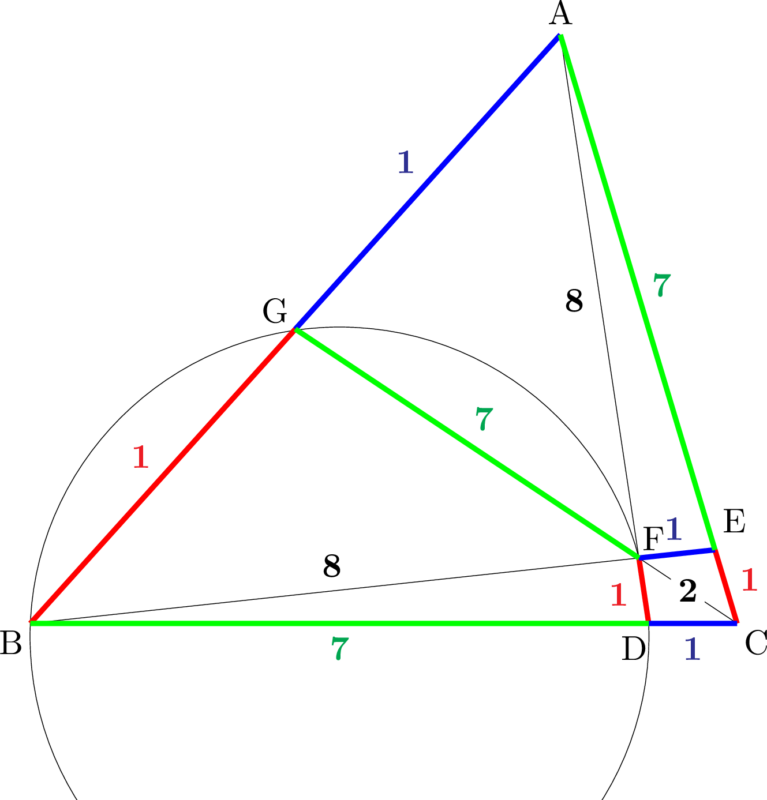



年センター試験 数学 A 第5問 平面図形 大学入試数学の考え方と解法
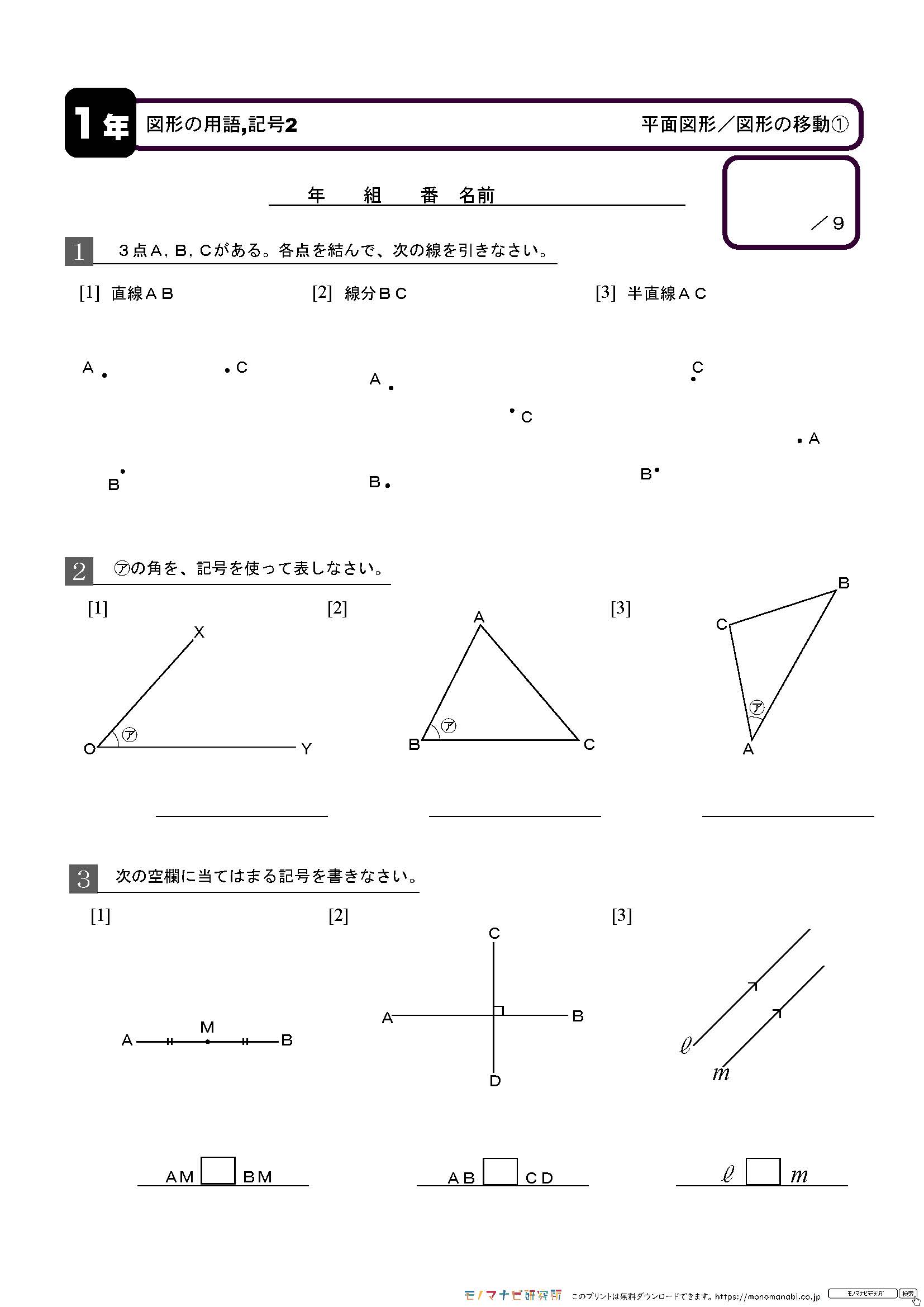



モノマナビ研究所




中1 数学 平面図形 中学生 数学のノート Clearnote



1
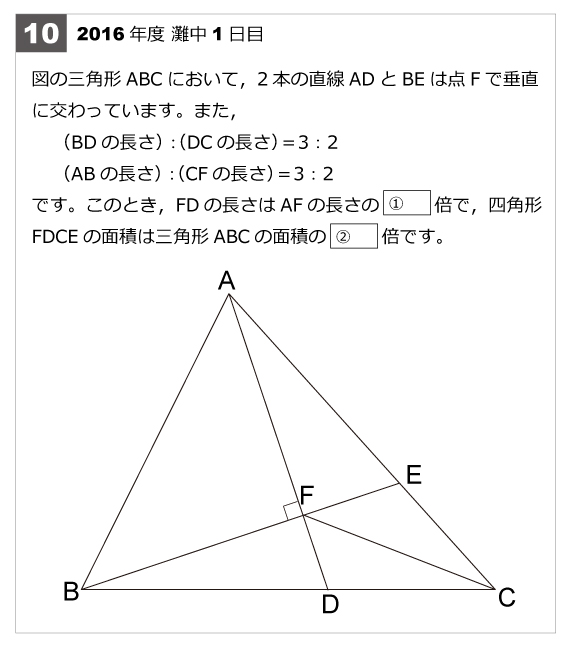



第10問 平面図形 難問 16年第10問 平面図形 難問 算数星人のweb問題集 中学受験算数の問題に挑戦




中1 数学 中1 80 空間内の平面と直線 Youtube




中1数学 多角形について 平面図形 ひっそりと物理や数学を解説する
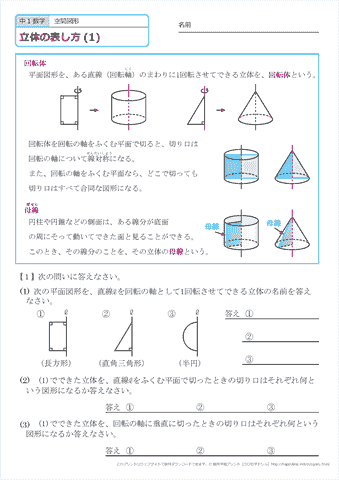



中学1年生 数学 空間図形 立体の表し方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年生 数学 平面図形の移動 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校1年 数学a 平面図形の問題です 4 と 6 の解答をお願い Clearnote




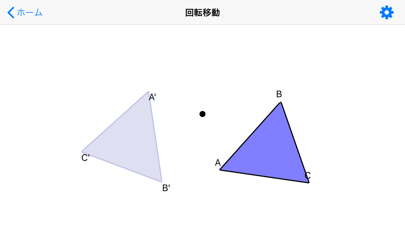
図形の回転移動の作図手順と性質 数学fun
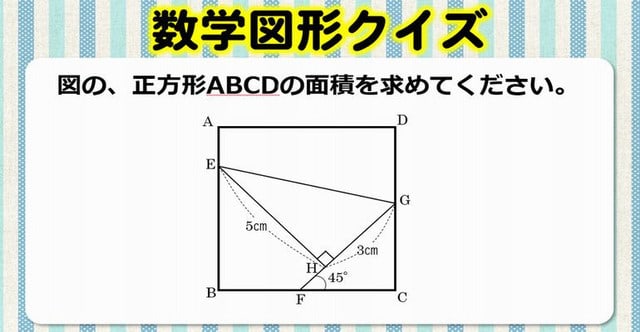



数学図形クイズ シンプルだけどひらめきが必要な正方形の面積の良問 暇つぶしに動画で脳トレ



中1数学 発展 応用問題プリント 平面図形の作図 136




数学ワンダーランド 本日オープン 数学美術館 平面図形 メルカリ




全都道府県 公立高校入試 過去問 数学 4 平面図形 1 角度の問題 在宅学習で高校受験対策




数学a 平面図形 円にまつまる問題チャート まとめ集 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru




中1数学 平面図形で知っておきたい図形の記号9つのまとめ Qikeru 学びを楽しくわかりやすく




数学の 平面図形の 最短距離の問題です 上が問題で 下が答えです Clearnote




中1 数学 平面図形 中学生 数学のノート Clearnote




中学受験 算数 平面図形 10 角度 Youtube



1




中1数学 平面図形 を攻略する3つコツ Qikeru 学びを楽しくわかりやすく



中1数学 基本 基礎問題 平面図形の作図 136




中学数学 平面図形と角度 の二等分線の裏技教えます 前半 中2数学 Youtube
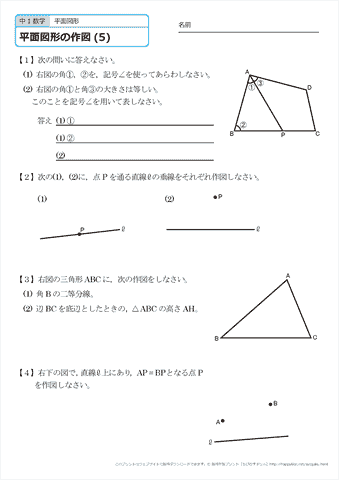



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 平面図形ノート 中学生 数学のノート Clearnote




中1数学 平面図形 を攻略する3つコツ Qikeru 学びを楽しくわかりやすく



中1数学テスト対策問題25 平面図形1 直線と角 対称 プリント




世界一わかりやすい数学問題集中1 5章 平面図形
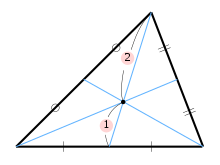



高等学校数学a 図形の性質 Wikibooks




数学 平面図形のコツ 新装版 Amazon Com Books
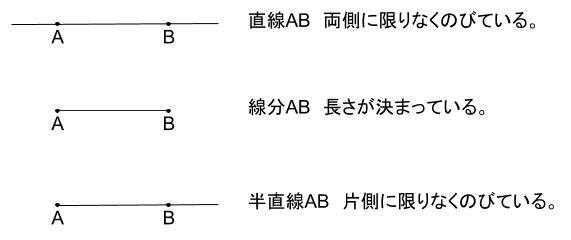



中学数学 図形用語の確認 中学数学の無料オンライン学習サイトchu Su
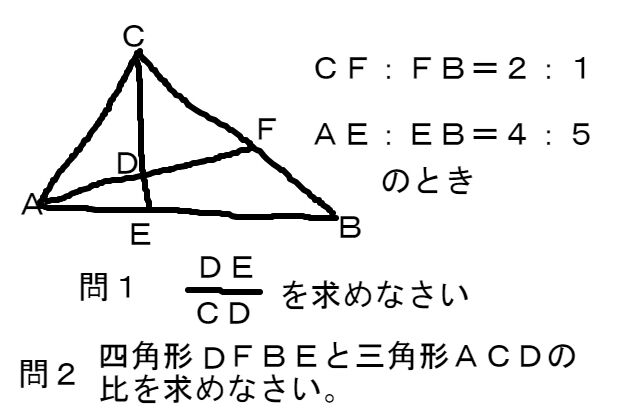



平面図形 応用問題 解答できれば素晴らしい 中学 数学 理科の復習サイト



中学数学平面図形 Apppicker




東京都立高校入試 共通問題 受験数学 平面図形制覇 Vもぎ手書き解説 メルカリ



無料 中1数学 標準問題 解答プリント 136 平面図形3 平面図形の作図




中学校数学 1年生 図形 平面図形 Wikibooks




オンライン教材 すらら 中学数学の平面図形は数学嫌いも最後まで頑張れる かつっぺblog




世界一わかりやすい数学問題集中1 5章 平面図形
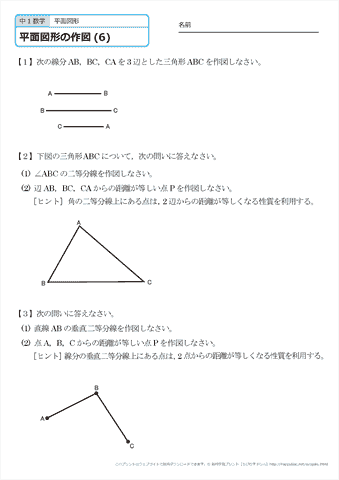



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 平面図形 のコツ 円とおうぎ形




高校入試の平面図形問題 でるのは3パターン これさえ押さえてバッチリ 高校入試徹底対策ガイド




円とおうぎ形 応用 無料で使える中学学習プリント




複素数平面 で解く 図形と方程式 杉本 幸司 数学 Kindleストア Amazon




中1数学 平面図形で勉強する 図形の移動 3つのまとめ Qikeru 学びを楽しくわかりやすく




平面図形15 メネラウスの定理 怜悧玲瓏 高校数学を天空から俯瞰する
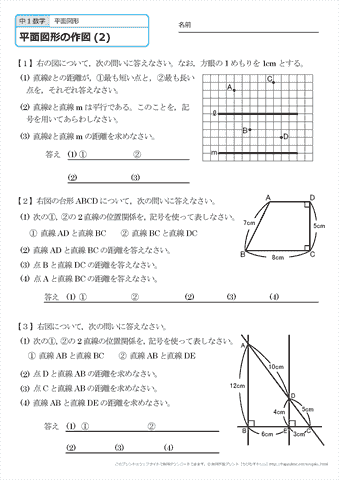



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1数学 図形の用語と記号 練習編 映像授業のtry It トライイット
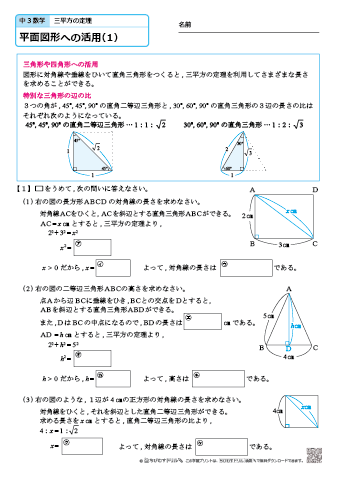



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生
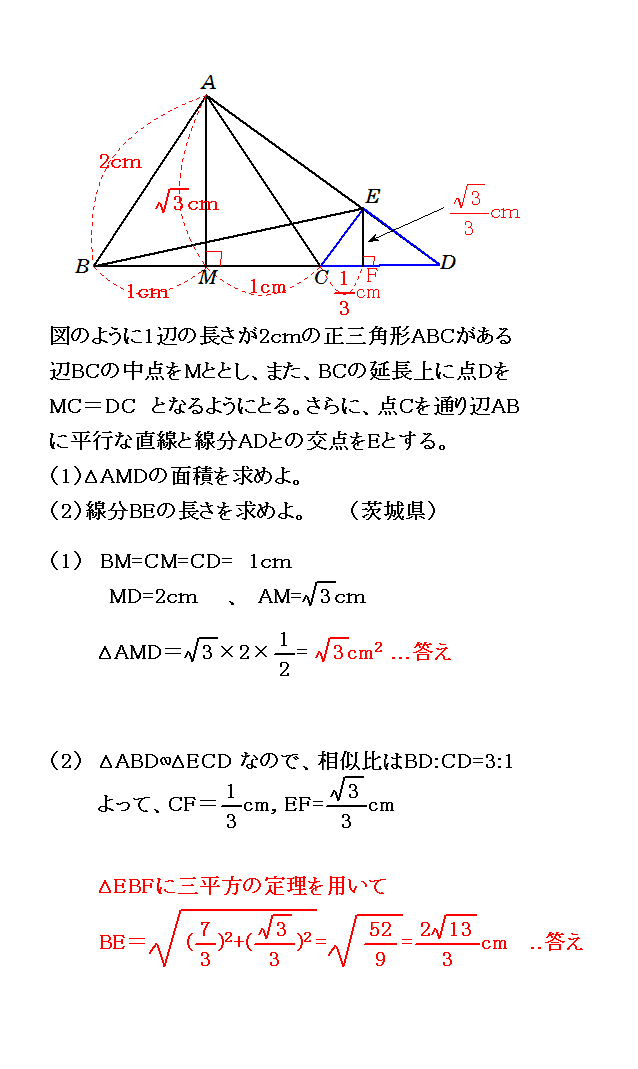



平面図形の問題 茨城県高校入試問題 ネコネコ算数数学ページ




高校の平面図形の問題です 角度を求める問題 Okwave




中1数学 平面図形で知っておきたい図形の記号9つのまとめ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿